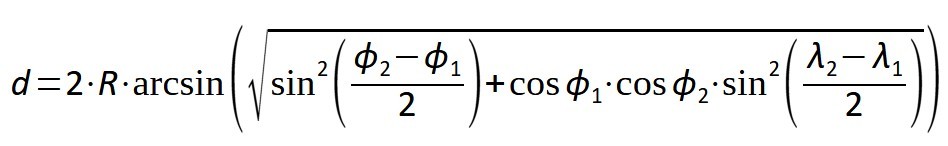Localisation
Localisation, cartographie et mobilité : du sextant au GPS
Tout point sur Terre se repère par deux angles : la latitude (φ, par rapport à l'équateur) et la longitude (λ, par rapport à Greenwich). Hier mesurées au sextant (latitude) et au chronomètre (longitude), elles sont aujourd'hui calculées par trilatération GNSS sur 4 satellites. Une fois la position connue, on la projette sur une carte (Mercator), on lit l'échelle, et on trouve le plus court chemin grâce à un graphe (algorithme de Dijkstra).
Formule de Haversine
LaTerre est (approximativement) sphérique.
La distance d‘entre deux points sur une sphère de rayon R estdonnée par la formule de Haversine :
Correspondance des symboles :
d : distance entre les deux points.
R : rayon terrestre moyen → 12742km/2=6371km
Φ1,Φ2 : latitudes des deux points (en radians).
λ1,λ2 : longitudes des deux points (en radians).
La formule de Haversine est précise pour de courtes et moyennesdistances. Elle est simple à implémenter.
Tableur
Python
from haversine import haversine,Unit
lyon = [45.7597, 4.8422] # (latitude, longitude)
paris = [48.8567, 2.3508]
distance_km = haversine(lyon, paris)
print(f"Distance: {distance_km} km")
# Solution sans utiliser de bibliothèque : haversine
from math import radians, sin, cos, sqrt, atan2
def haversine_math(lat1, lon1, lat2, lon2):
# Rayon moyen de la Terre en mètres
R = 6371000
# Conversion des coordonnées en radians
lat1, lon1, lat2, lon2 = map(radians, [lat1, lon1, lat2, lon2])
# Différences de coordonnées
dlat = lat2 - lat1
dlon = lon2 - lon1
# Formule de Haversine
a = sin(dlat / 2)**2 + cos(lat1) * cos(lat2) * sin(dlon / 2)**2
c = 2 * atan2(sqrt(a), sqrt(1 - a))
distance = R * c
return distance
distance_km = haversine_math(lyon[0],lyon[1], paris[0], paris[1])
print(f"Distance Math: {distance_km/1000} km")